Introduction
Factors are integral to mathematics, serving as the building blocks that, when multiplied together, yield a target number. But their significance extends beyond numerical exercises.
In this article, we explore the multifaceted effects of factors, from their role in mathematical applications like control theory to their impact on societal structures and resource distribution. Join us as we delve into the fundamental concepts and real-world applications of factors, providing practical insights and solutions for CFOs.
What Are Factors?
Factors are integral to mathematics, serving as the building blocks that, when multiplied together, yield a target number. For instance, the factors of 6—1, 2, 3, and 6—combine seamlessly to produce 6 without any remainder.
This concept transcends mere numerical exercises; it underpins various societal structures and influences a myriad of fields. Control theory, a mathematical discipline shaped amidst wartime politics, exemplifies the profound impact of mathematical applications.
Moreover, the use of mathematics extends to organizing and safeguarding societal segments. Yet, its deployment is not without controversy.
For example, the Gaussian copula, a mathematical function crucial to financial risk models, was pivotal in the 2008 financial crisis. Mathematics also plays a role in the distribution of resources, which can have significant moral, legal, and ecological ramifications. The extraction of resources, a process influenced by mathematical decision-making, can lead to benefits for some while disadvantaging others. These examples underscore the multifaceted effects of mathematics on our world, highlighting the importance of understanding fundamental concepts like factors.
Factors of 6: A Detailed Explanation
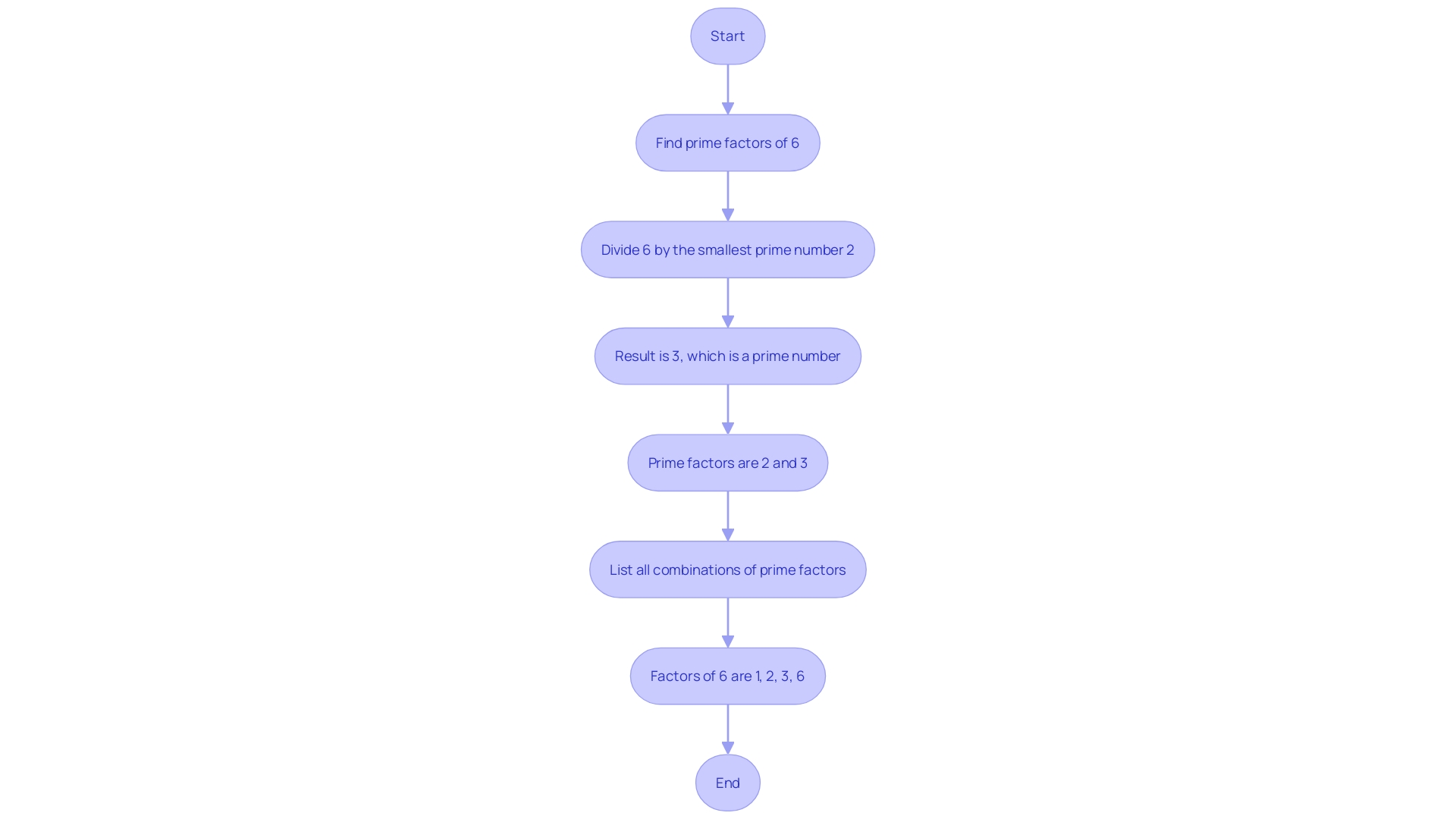
To grasp the concept of the factors of 6, it's crucial to dissect the number into its elemental components, the prime factors. These prime numbers, specifically 2 and 3 in the case of 6, are the unique building blocks that, when multiplied together, construct the number 6.
The factors of 6, therefore, include 1, 2, 3, and 6 itself. Each of these factors pairs with another to form the product of 6—2 pairs with 3, and 1 pairs with 6.
It's an intriguing mathematical truth that prime numbers such as these are the atoms of mathematics, forming the very foundation of our numerical system. Furthermore, prime numbers hold a place of mystery and significance in mathematics, with their distribution being a million-dollar question in the form of the Riemann hypothesis. Recognizing the factors of 6 is not just an exercise in multiplication; it's an exploration into the fundamental principles that govern the realm of numbers.
Divisors of 6: A Mathematical Perspective
Understanding the divisors of a number is a fundamental concept in mathematics, pivotal for various computational and theoretical applications. For the number 6, its divisors are the integers that divide it without leaving a remainder: 1, 2, 3, and 6.
These are the building blocks that, when multiplied together in different combinations, give us the product 6. The divisors of 6 are particularly interesting as they represent a simple case of the intricate interplay between numbers that mathematicians and computer scientists explore.
In the realm of tropical geometry, for instance, the concepts of optimization and geometry converge. Here, the factors of 6 could serve as a straightforward example of how numbers interact within geometric spaces.
Moreover, in the world of linear programming, millions of calculations are processed globally every day, where the understanding of numbers like 6 and their properties can significantly impact algorithmic efficiency and complexity. The geometric representations of problems in linear programming, known as polytopes, are directly tied to factors and divisors. They describe feasible regions and are essential in optimizing outcomes, such as setting prices in auctions to maximize seller profits. These divisors, while simple, are a part of the larger mathematical tapestry that drives innovation across disciplines, including “Topological Data Analysis,” where data is analyzed through the lens of topology using numbers and their properties. Therefore, the divisors of 6 are not just numbers; they are tools that unlock a deeper understanding of mathematical structures and their applications in computational research and beyond.
Real-World Applications of Factors of 6
Factors and divisors are more than mere numbers; they are the building blocks of mathematical concepts and real-world applications. In the realm of mathematics, understanding factors is key to prime factorization, which simplifies complex problems into their elemental parts, revealing the properties of numbers. This knowledge is extended into engineering, where factors such as dimensions and materials are critical in product design and production.
In the financial sector, factors are indispensable in dissecting financial statements and informing investment decisions, where profitability, liquidity, and solvency are scrutinized. The influence of mathematics, however, transcends the classroom. It plays a pivotal role in societal structures, such as the development of control theory, which has roots in wartime innovation.
Mathematics also aids in organizing and safeguarding societal aspects, evidenced by its application in creating or dismantling transportation networks. Moreover, it has profound effects on social dynamics, where grading systems may inadvertently reflect a student's socio-economic background. The Gaussian copula, a mathematical function, was notably instrumental in the 2008 financial crisis, illustrating how mathematical tools can have far-reaching consequences.
Mathematics also intersects with the political landscape, shaping the extraction and consumption of natural and economic resources. It can lead to significant advantages for some, while creating imbalances for others, raising questions about its ethical and ecological footprint. As new mathematical applications emerge, they bring with them a spectrum of societal impacts, from resource management to the politics of artificial intelligence, underscoring the inherent dynamics of mathematics in our world.
Conclusion
In conclusion, factors are fundamental in mathematics and have far-reaching effects. They serve as building blocks and have practical applications in fields like control theory.
The Gaussian copula's role in the 2008 financial crisis emphasizes the importance of understanding mathematical tools. Factors and divisors go beyond numbers; they unlock a deeper understanding of mathematical structures.
They are applied in prime factorization, engineering design, and financial analysis. CFOs can leverage this knowledge to make informed decisions.
Mathematics also influences societal dynamics, from transportation networks to grading systems. It intersects with politics, shaping resource distribution and raising ethical questions.
CFOs must grasp the multifaceted effects of factors. By using this knowledge responsibly, they can drive positive change while considering broader implications. In summary, factors play a crucial role beyond mathematics. They impact various aspects of our world, from finance to resource distribution. CFOs should understand their significance and use them as tools for informed decision-making. By doing so, they can drive positive change while considering ethical dimensions.




